While Quackle is largely known for its kibitzer and simulation engine, there are other features of Quackle that are very important and can be valuable tools that can help you improve your game. This article will be an overview on these features along with their strengths and weaknesses, and how you can use these alternative features to win the game.
The Endgame Engine
During the endgame, basic simulation heuristics are not good enough: an entirely different method of Scrabble analysis must be used. For this reason, Quackle comes with an endgame engine used to solve endgames and evaluate preendgame plays that empty the bag.
The endgame engine is much stronger than humans, especially during the endgame, and can correctly identify the exact percentage that bag-emptying plays win during the preendgame most of the time, making it an extremely powerful tool. Computers are far stronger and faster than humans at endgames due to its remarkable raw processing speed and its ability to go through each possible draw and endgame extremely quickly. Quackle solves around 98% of endgames correctly.
This is performed by clicking the “Ask Championship Player for Choices” button, in which case Quackle will give you accurate win% as long as there are 2 or less tiles in the bag after your play. Sometimes it will take a minute, so be patient. Quackle will actually play every single possible turn until it finds the best play, using rote computer power. Think of it as a simulation that simulates every single combination of plays and finds the exact score. During the normal game that is not possible, but at or near the end of the game, there are a lot less possibilities.
This being said, there *are* times where Quackle analysis is imperfect. One reason for Quackle errors is because the position might involve a play that is not on Championship Player’s radar, because the move scores extremely poorly. Championship player can only permute between the top 50 plays in equity. A secondary reason for miscalculation are endgames that require many, many plays, such as trap endgames or endgames that involved extremely clunky racks. An example of each type of endgame is listed below:
| Diagram 1: | Diagram 2: |
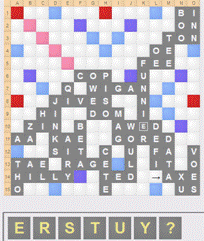 | 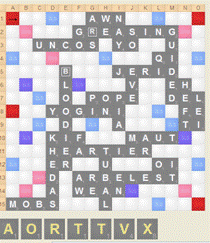 |
| Score: 310-357 | Score: 380-412 |
| Pool: LMNPRRR | Pool: CNZ |
| An endgame requiring a low scoring play (NUTS 8k (4)) | A trap endgame that Quackle misplays |
The endgame engine is an extremely useful tool to improve your endgame, helping you to practice finding optimal routes. New endgames can also easily be generated by simply changing the letters in your rack. This can prove to be a great way of practicing endgames or even pre-endgames with one or two tiles in the bag. By going back and changing even one play, you can create a number of different endgames with different themes from one base position!
Inference Engine
If you are an advanced player, the chances are good that you know how to use leave inference to deduce a range of likely tiles your opponent might be holding. Using this information can sometimes produce radically different simulation results and provide different insights that can help you improve your strategy. (Leave inference is further discussed in my book Words of Wisdom.)
Most of the time, you don’t have knowledge of your opponent’s exact tiles, but rather you have an idea of their leave depending on their plays. Thus, you may need to plug in an assortment of leaves depending upon the likely range of opponent’s racks, and run a series of simulations to use the inference engine to its maximum. The inference engine is also extremely useful when trying to figure out an accurate bingo percentage for your opponent and figure out whether or not you should block certain bingo opportunities, as it is much more realistic in many cases than assuming a random rack.
The implication engine can be used by going to the ‘Choices’ tab and checking the box that says “Specify partial oppo rack’, then plugging in the letters you believe your opponent might have, and then running a simulation. A picture illustrating the implication engine is shown below:
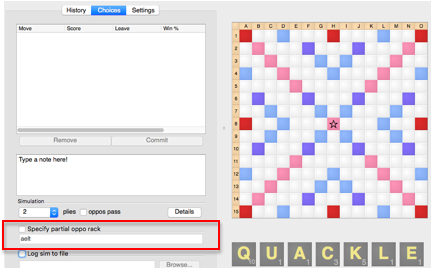
The Details Box
Many Quackle users use simulation as a very result-oriented process: they run a simulation, log the result, and move on. However, players who use Quackle in this way are missing out on learning as much as they can from the simulation that they run, using the additional data available in the details box.
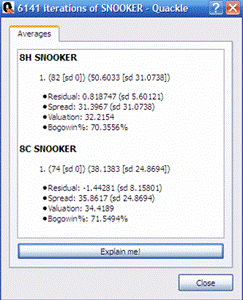
The details box separates the simulation into various components, giving you some useful statistics to evaluate the position. To illustrate, here is some data on the opening rack SNOOKER.
SNOOKER 8h: Row 1: (82 [sd 0]) (50.6033 [sd 31.0738])
SNOOKER 8c: Row 1: (74 [sd 0]) (38.1383 [sd 24.8694])
The first number is your score. SNOOKER at 8h scores 82, while SNOOKER at 8c scores 74. The second number is sd, which stands for standard deviation. The standard deviation is a function of statistics, and measures the volatility of that score, which is somewhat akin to a measure of short term entropy. The standard deviation of our plays is zero: after all, we are guaranteed either 82 or 74 points, depending on what plays we choose.
The second score is your opponent’s mean score. It is the average number of points that your opponent scores in the ensuing position. The standard deviation measures the range of these scores: again, the higher the sd, the larger the range. After SNOOKER 8h, this is obviously a higher number, since they can score well with the blank or the S, but have few scoring options without blank or the S. In this case, SNOOKER 8h not only gives back more points: it is also more entropic.
SNOOKER 8h: Row 2: Residual: 0.818747
SNOOKER 8c: Row 2: Residual: -1.44281
The Residual refers to the mean difference in leave between you and your opponent. It is the value of your leave minus the value of your opponent’s leave at the end of the simulation. In this case, after a bingo, your leave value is going to be pretty close to zero, so we are mostly measuring your opponent’s leave. 8h should have a higher residual than 8c as your opponent is going to have a weaker leave after 8h than 8c since they will often hold onto their S or blank if they can’t bingo after SNOOKER 8c, but they will use their S or blank if you play SNOOKER 8h.
SNOOKER 8h: Row 3: Spread: 31.3967 (sd 31.0738)
SNOOKER 8c: Row 3: Spread: 35.8617 (sd 24.8694)
The spread is the mean difference in score after both you and your opponent play, without regard to your leave. Since SNOOKER at 8h scored 82, that means the mean difference in score will be 31.3967, and the mean score will be 82 to 40.6033, in your favor. The Standard deviation of spread is the volatility in the differences between you and your opponent’s score. In a 1-ply sim it will be the same standard deviation as your opponent’s play, but in a longer sim it will be larger than any single standard deviation.
The spread also takes into account the score at the time. Since the score starts at 0-0, it does not matter. If you were down 100-0 before this play, then both spreads would be negative even after your bingo.
SNOOKER 8h: Row 4: Valuation: 32.2154
SNOOKER 8c: Row 4: Valuation: 34.4189
Valuation: This is the value of your play, averaging the scores of all of the plays that you have accumulated over the simulation, the scores your opponent has accumulated over the simulation, and the leaves each of you possess.
As you can see, all of the stats in the Details Box are all related to each other, and you can calculate many of them if you know the others.
SNOOKER 8h: Row 5: Bogowin%: 70.3556
SNOOKER 8c: Row 5: Bogowin%: 71.5494
This is your win% as calculated by the table Bogowin, which functions not too different from superleaves. Bogowin uses the number of tiles remaining and the difference in game score after each iteration and pulls out a table to look at your win percentage, then averages those win percentages together. Since this is simply a function of game score and tiles remaining, you shouldn’t take this number too literally.
While it can be useful to help Quackle play better, it is useless in trying to help you figure out what the best play is until you get to situations where 2 or less tiles are in the bag, when Bogowin is replaced by a separate preendgame player.
Bogowin is a program that is used to account for volatility. Basically, the makers of Quackle decided that it would calculate values for your odds of winning the game on average if there are T tiles in the bag and you are ahead by G points. So they ran a giant simulation on all possible boards, and developed a large database consisting of every spread up to + or – 200 points and your odds of winning with a given spread depending on how many tiles were remaining in the bag. Bogowin runs every single Spread at the end of the simulation into Bogowin, and it spits out a win% according to its database. These win% numbers are then averaged.
While this seems like a good idea and it certainly is an approximation, it is a rather poor approximation. Being up 100 on an open board with 40 tiles in the bag is a lot worse than being up 80 with 50 tiles in the bag on a very closed board. Humans are ultimately much better judges of win% than computers until the preendgame.
Conclusion
Many players just only use Quackle’s kibitzer and simulation engine, but there are many more useful features of Quackle that can not only help you analyze games, but can help you make better approximations and quantifications and develop your intuition. [For example, the details box can help you develop your intuition about entropy and bingo percentage (especially when used with the implication.)] To get the most out of computers, it is important not to just use simulation, but to use the other tools to enhance your understanding of Scrabble.
