This is the first installment of the “Controlling Chaos” series on entropy. For a list of all articles in this series, please click here.
When making an investment or decision, there are two things that are important: worth and risk. In general, worth is expressed as expected value while risk expresses the range of possible. Balancing these factors is essential when trying to make monetary, professional, personal, and game decisions.
These concepts can be applied to Scrabble. A play’s worth can be approximated as the sum of points and leave, although there are certainly a multitude of other factors. Risk also plays a prominent role. For example, a play that opens a triple-triple alley is very risky since it could result in a huge score, but it typically has little effect on worth since triple-triples are fairly unlikely. In Scrabble, risk is assessed in terms of entropy.
Entropy measures the ability for a trailing player to overtake their opponent in score. In statistical terms, entropy can be equated to the variance of score difference between you and your opponent, or the likelihood of large scoring swings to occur. When behind, entropy is desirable as it increases the likelihood of catching up (as well as your chances of getting blown out). When ahead, entropy is undesirable since it allows your opponent to win if he is fortunate enough to draw well. (When the score is tied, entropy is neither desirable nor undesirable.)
Entropy should be considered alongside equity. When comparing two plays, many players find it helpful to think of entropy and equity as an ordered pair, where both factors are taken into account. Sacrificing equity in order to attain a more desirable entropy level is an important part of Scrabble strategy.
Entropy is usually divided into two categories: rack entropy and board entropy. As the name implies, rack entropy assesses the fluctuations of your future score with a specific rack. High entropy racks include racks with heavy bingo potential as well as imbalanced leaves such as AEI. Rack entropy situations show up fairly frequently, but since tiles are played very quickly, rack entropy only matters for one or two turns.
Board entropy assesses the ability for the score to change on a specific board. High entropy boards have few scoring spots but many bingo lines. Board entropy can vary greatly both in the long and short term: bingo lines can be thought of as “currency” for short term entropy while space and board dynamics are the “currency” for long term entropy.
When making decisions about entropy, there are a number of factors that you must take into consideration, including:
- Game score: When behind, you should usually increase entropy, while you should usually decrease entropy when you are ahead. Increasing or decreasing entropy also depends on your propensity for either you or your opponent to outscore a bingo.
- Stage of game: As the game progresses, entropy becomes significantly more important as there is less time for random chance to affect the outcome of the game.
- Long term ramifications: It is important to observe the situation and determine if you can significantly affect entropy. If there are two bingo lines open and you want to block one of them, will your opponent be able to viably make bingo lines on future turns? If so, it is probably not worth reducing entropy for one turn: the benefits of entropy are only substantial if they last.
- Opponent skill level: The more skilled your opponent, the more you want to increase entropy. Against less skilled opponents, entropy is a much less important factor, since they might do some of the work towards you.
- Opponent tendencies: Does your opponent try to reduce risk in high-entropy situations, even when they are not supposed to? Do their actions depend on what type of tiles they have?
- Not all bingo racks have high entropy.
- Not all scoring racks have low entropy.
- Gambling to finish your opponent. Ideas such as “taking a shot to end the game” or “taking a risk because you can afford it” are completely wrongheaded, and are diametrically opposed to what you should be doing whenever you have an advantage.
- Decreasing entropy out of fear. Many players block bingo lines, X spots, or big openings out of fear rather than calculation. There need to be concrete reasons for decreasing entropy, especially if you don’t have a lead: just because a risk exists does not mean it needs to be minimized.
- Entropy can be thought of exclusively of equity. Entropy should never be thought of independent of equity: you are paying equity to control entropy. While entropy is an important factor, at the end of the day it’s important to always consider equity. If you’re up by 50, there might be a 10 point play that reduces entropy and drops your opponent’s bingo chances from 10% to 2%, but if there’s a 45 point play available, that 8% difference in bingo probability doesn’t even matter.
- Decreasing scoring spots usually does not decrease entropy. Entropy is not a measure of the ability to score: it’s a measure of the “variance” of one’s ability to score, and often times scoring spots decrease that variance, since they serve as a stopgap between bingos and ugly racks. Blocking scoring spots usually does not decrease entropy: in fact, many times it actually serves to increase entropy.
- How you should control entropy only depends on whether you are ahead or behind. Controlling entropy depends on other factors such as your tiles, the tile pool, and point spacing. The potential of attaining a 70 point bingo is far more significant when the average non-bingo scores 20 points rather than 40 points.
- You can’t control entropy for the entire game. Smart, adapting opponents can take huge advantage of this strategy so long as they know what to do. 40 point leads on turn 3 are rarely worth protecting enough to risk significant equity in exchange for control of entropy.
Graphical Representation
Like any variable, entropy can be calculated. While the math of entropy is very complex, its effect can be brought to light by using Quackle to formulate a data set and representing that data set graphically.
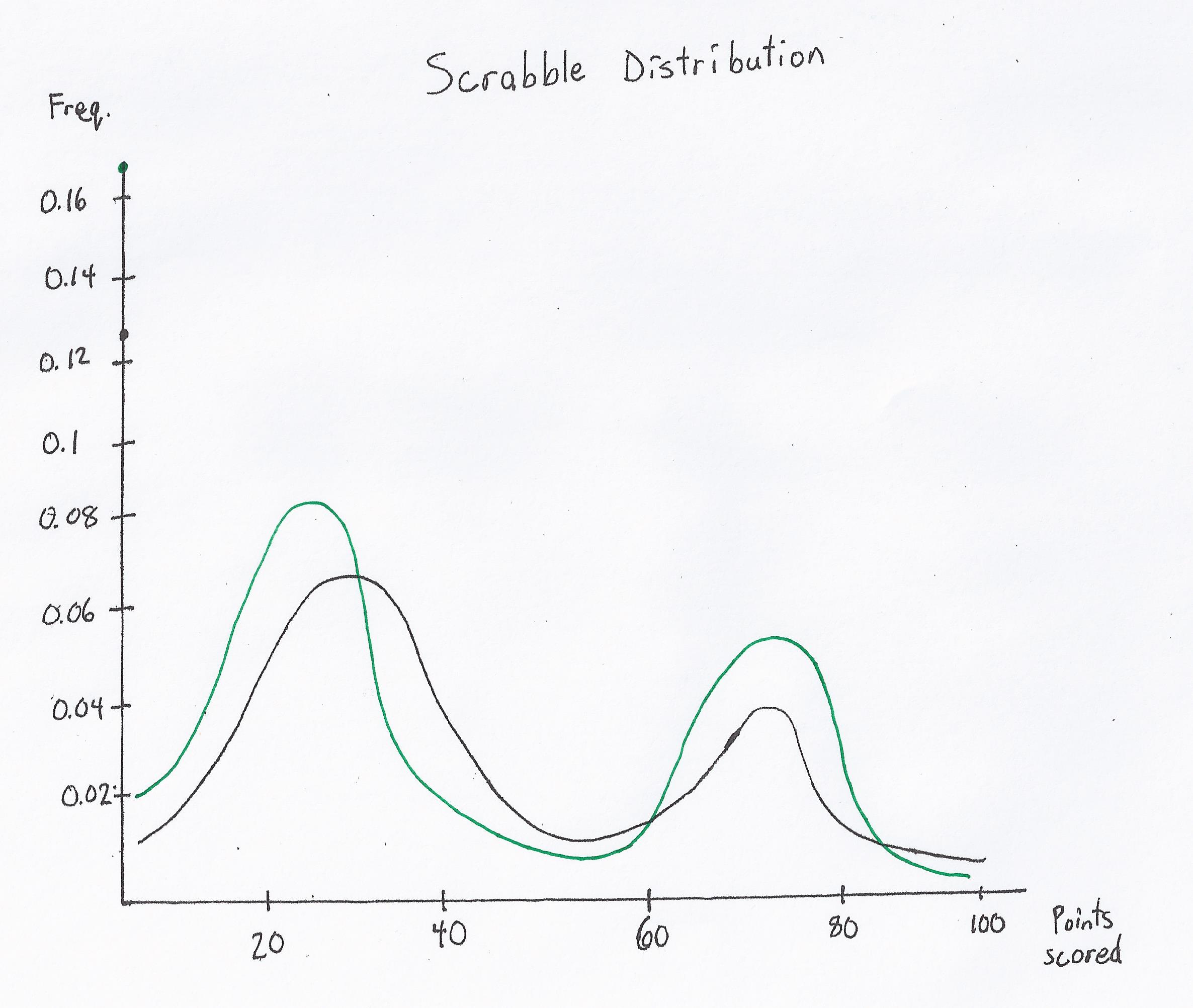
First, let’s begin by looking at a basic Scrabble distribution, assuming a random rack at a random time of the game.
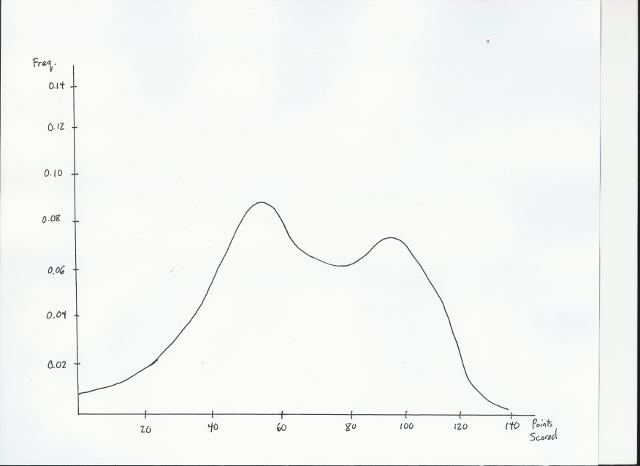
Scrabble Distribution
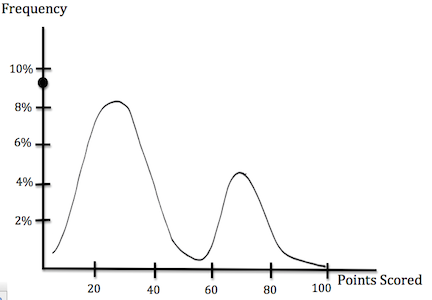
As you can see, the Scrabble distribution is largely Gaussian, but with two humps: one bell curve representing the score of the non-bingo plays, while the other bell curve represents the score of bingos. Entropy is represented by the point differences between both curves, and can often be approximated by the difference between the local maxima.
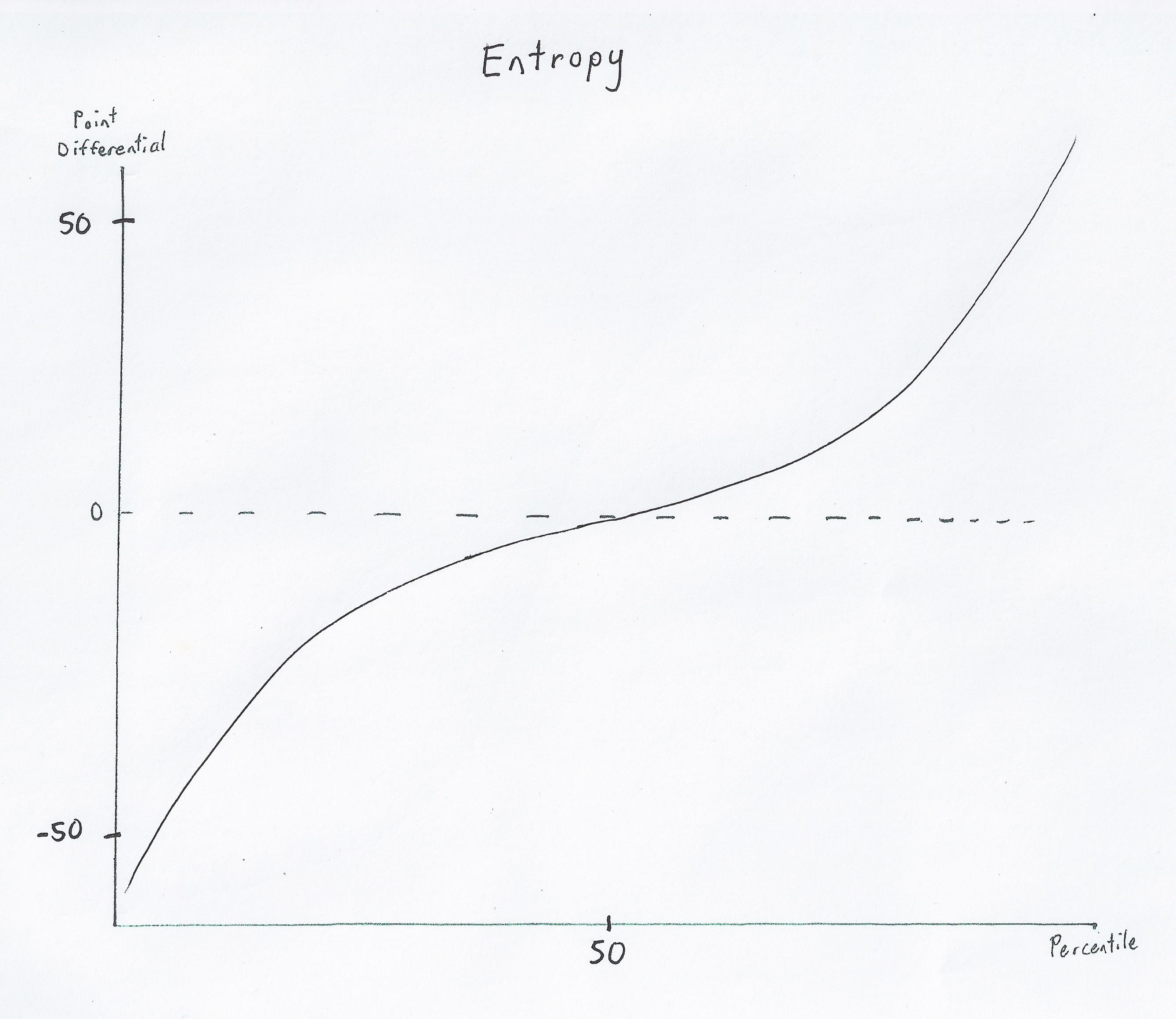
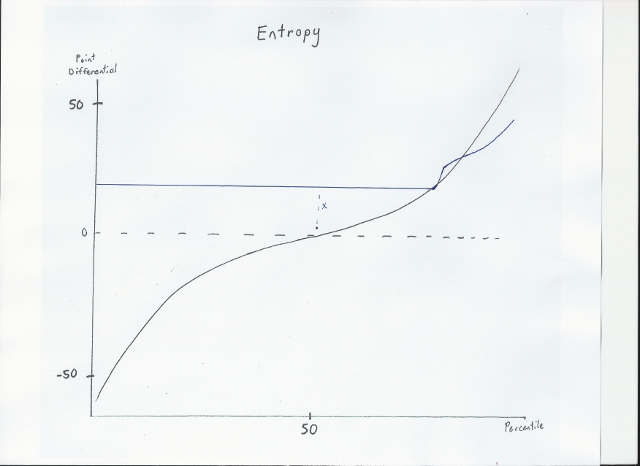
Entropy Graph
This graph represents the difference in two random scoring plays. When we want to reduce entropy, we want to cause the graph to converge to the central dotted line. When we want to increase entropy, we want to cause the graph to diverge away from the central dotted line. The slope of this graph is dependent mostly on the board and your leave.
Entropy effect
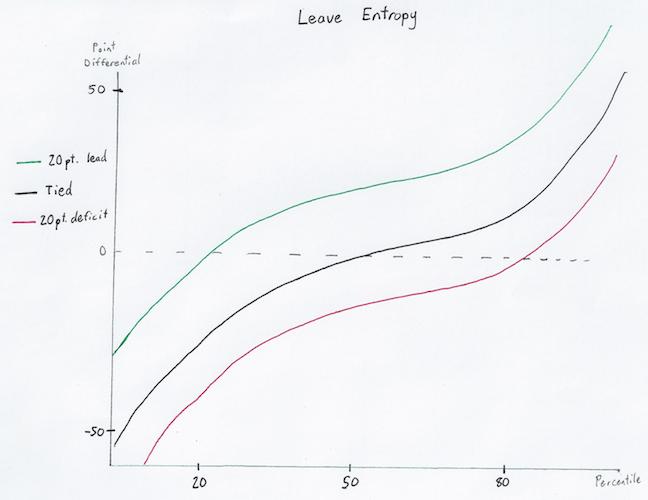
Here is the same graph showing entropy and its effect given the game score. As you can see, without a bingo it is fairly difficult to make up large deficits, because of the flat portion towards the middle of the entropy graphs.
| Scoring Leave Distribution: | Entropy Graph: | |
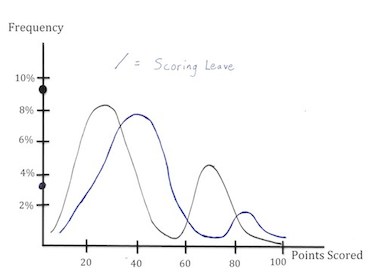 |
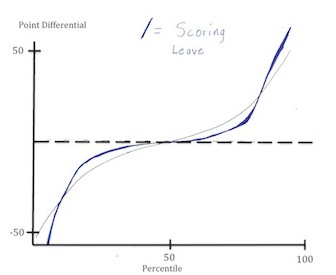 |
On the left is the distribution of a scoring leave or a low entropy board. On the right, you can see the entropy. Scoring leaves or low entropy are thus great for maintaining a lead, but not so great for overtaking a deficit.
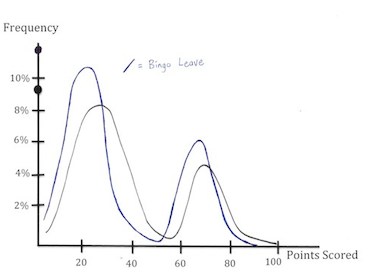
| Bingo Leave Distribution: | Entropy Graph: | |
 |
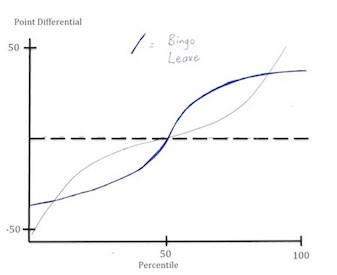 |
On the left is the distribution and entropy of a bingo leave or open board. As you can see, there is a huge void of scores between 35-60 points, creating a huge entropy.
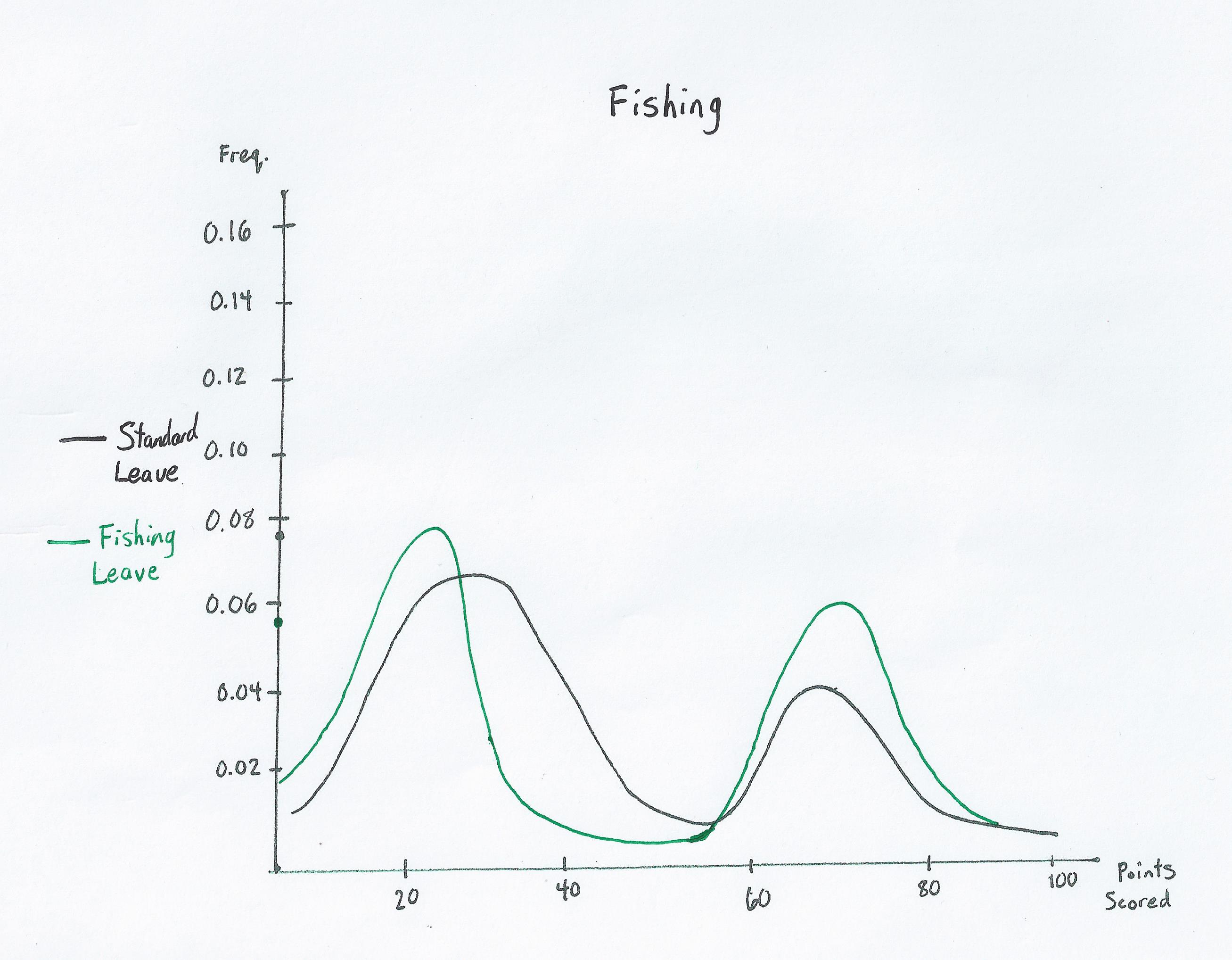
| Fishing Distribution: | Fishing Entropy Graph: | |
 |
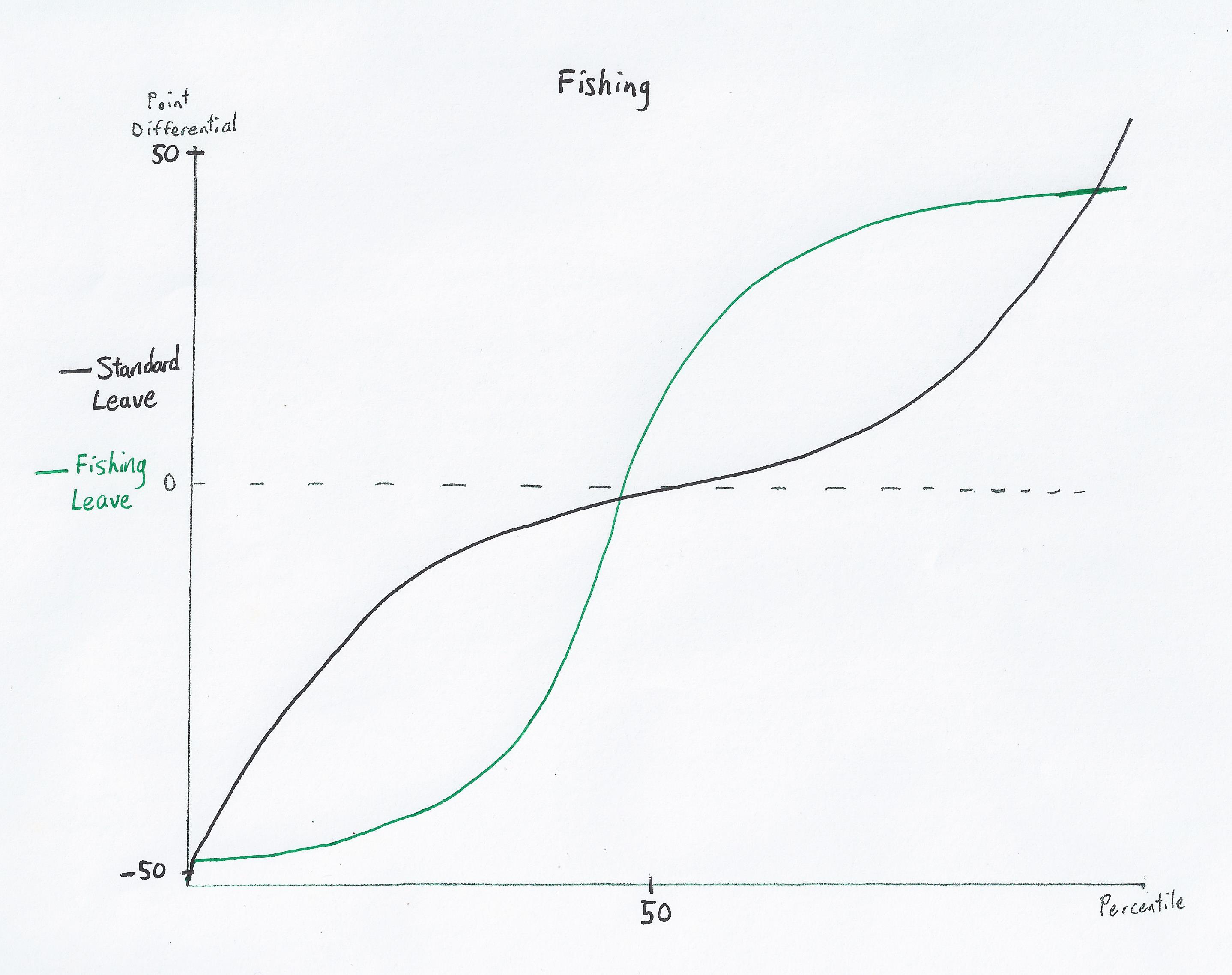 |
Unsurprisingly, fishing is very similar to a strong leave, as you can see with the fishing distribution and entropy graphs.
| Scoring Setup Distribution: | Scoring Setup Entropy | |
 |
 |
The setup graph might seem a bit strange, but this is because of the unique nature of setups when they are unlikely to be blocked: they are often nearly guaranteed. Because of that, the entropy is extremely low when the setup cannot be blocked, and depends on whether or not the setup is easily detected.
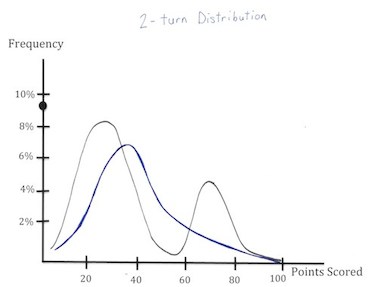
| 2 turn Distribution: | 2 turn Entropy | |
 |
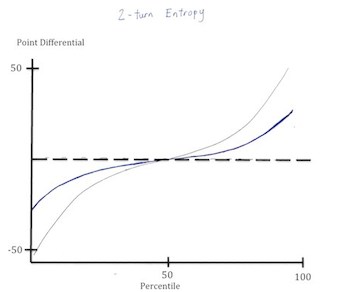 |
Obviously, the additive effect of entropy over time does lessen its effect. For example, if you have a strong bingo leave (such as EIRST) on a somewhat open board, eventually you are going to convert that rack into a bingo. While there are ways to affect long term entropy, these changes provide a skew and not a drastic change in polarization.
Examples:
While entropy is often quite intuitive when assigned to various leaves, it is often far less intuitive when it is ascribed to various boards. Thus, I have created a few sample boards and distributions to help illustrate how this applies to Scrabble. Here are some examples of an how entropy can be ascribed to different board situations:
| Board 1: | Distribution Graph: | |
 |
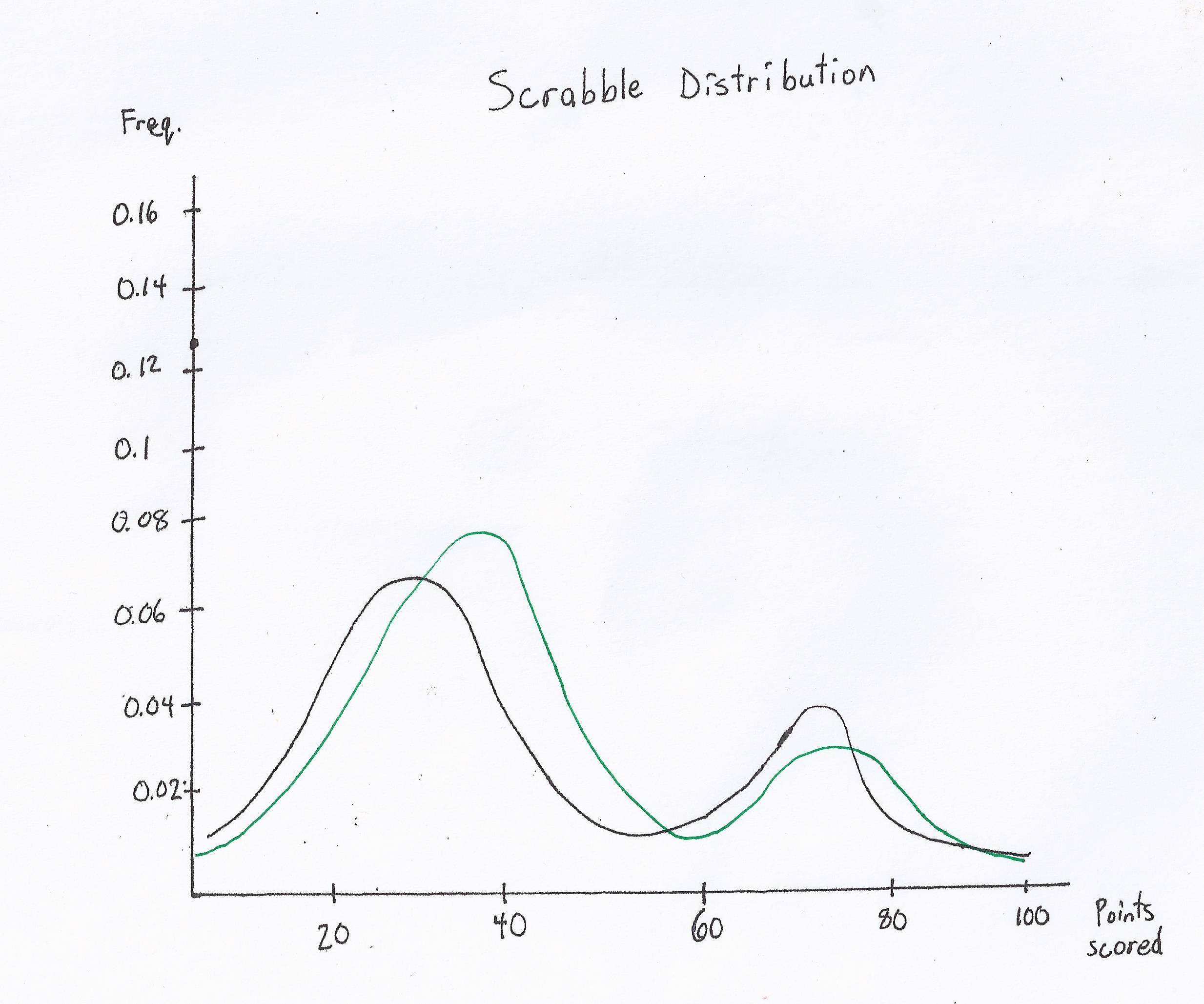 |
This is an example of an open board with a low entropy. Here, there are many scoring and bingo opportunities, and the bingo opportunities are not far outweighed by the scoring opportunities: thus, it can be difficult to make up a large lead.
| Board 2: | Distribution Graph: | |
 |
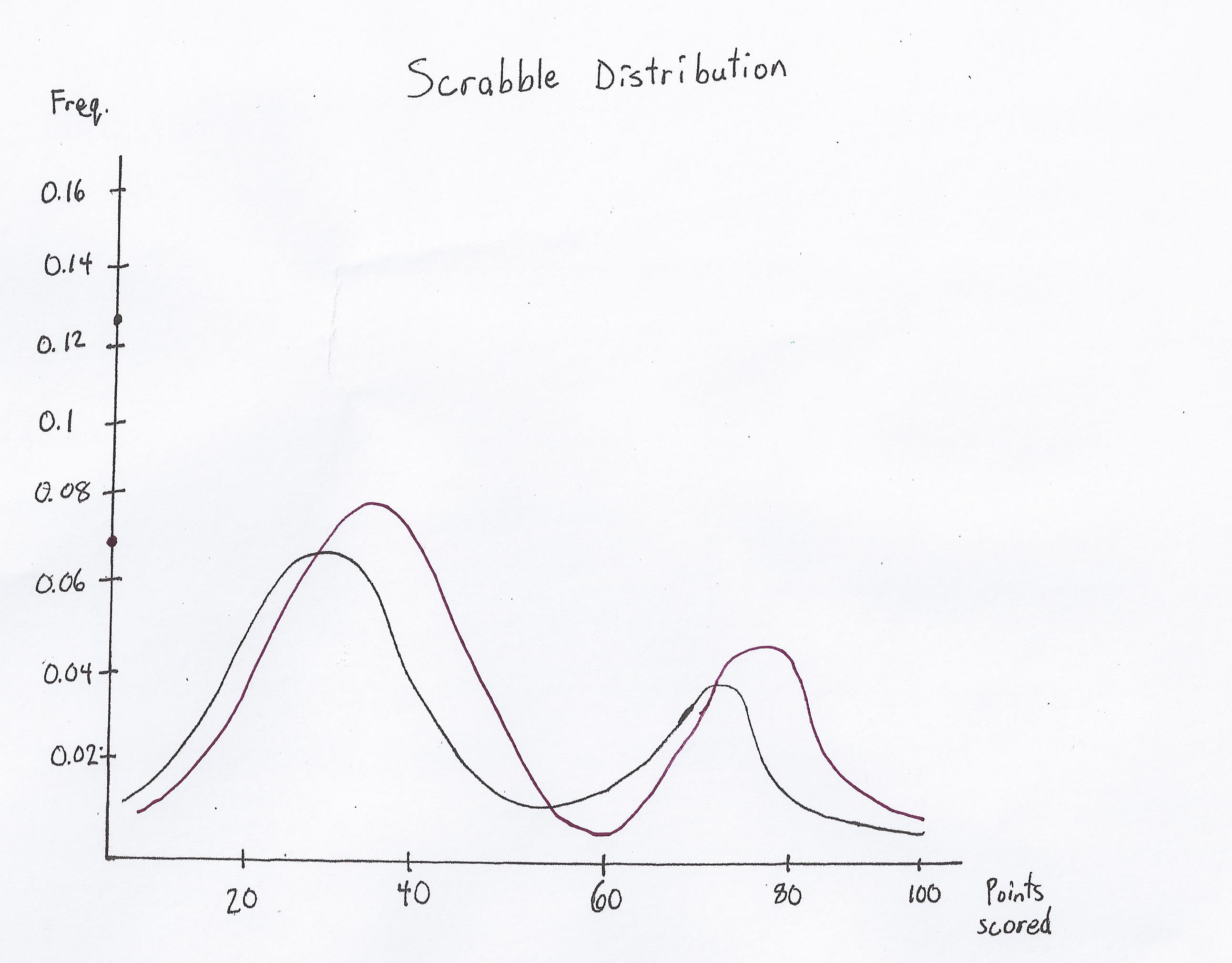 |
This is an example of an entropic open board. Here, there are plenty of bingo lines available but the opportunities are much more for bingos than scoring, as it is difficult to score with high point tiles on this board.
| Board 3: | Distribution Graph: | |
 |
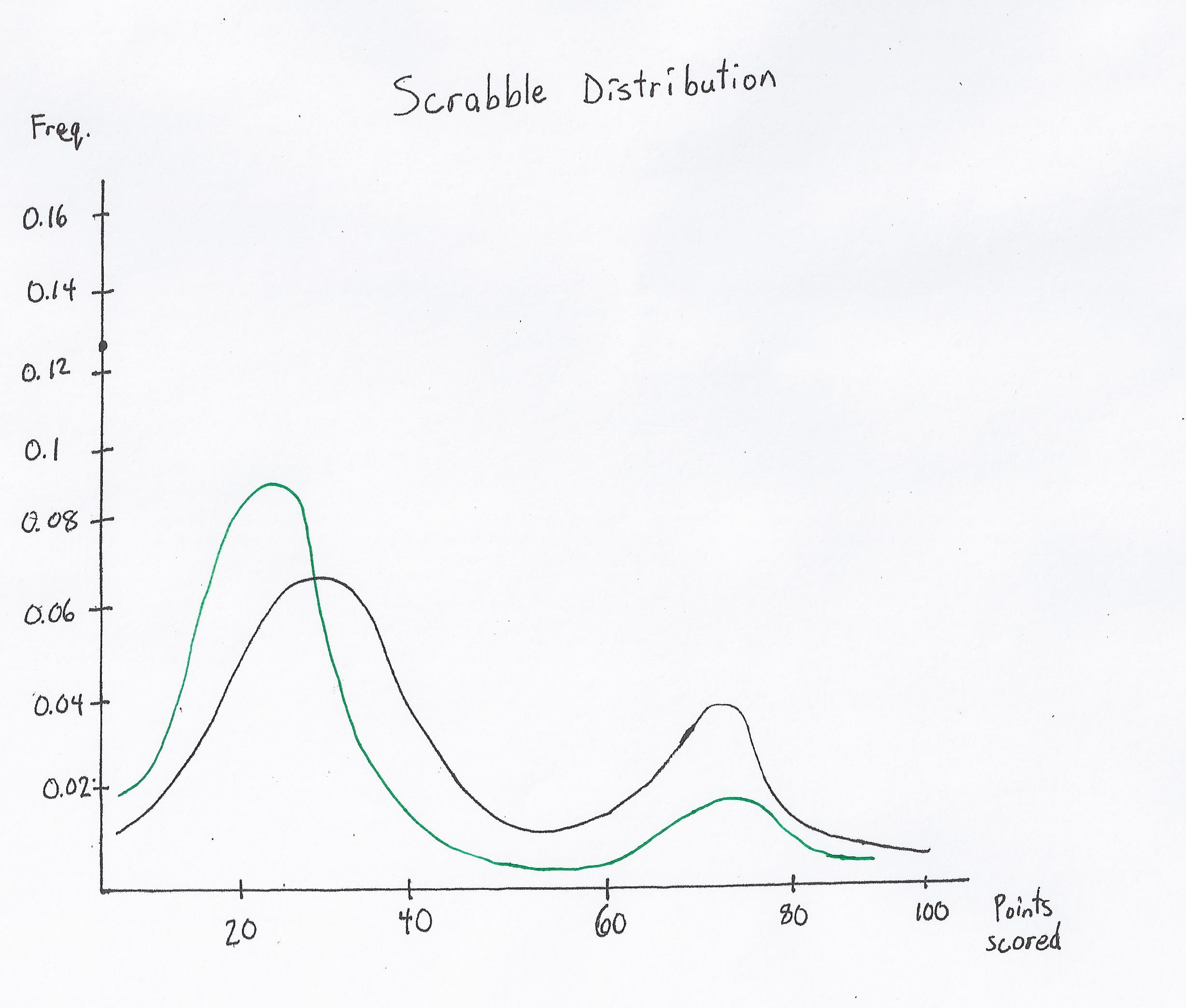 |
This is an example of a typical closed board. There are a few scoring options available but not much in terms of bingo options, and swings in this game will be fairly minimal.
| Board 4: | Distribution Graph: | |
 |
 |
This is an example of a volatile closed board. While there are few scoring options there are potential bingo options, many of which will be difficult to block without substantial sacrifices in equity.